Distance Loss for Ordinal Classification

Deep Learning

Informations


Introduction

Cross-entropy (CE) is extensively used in data classification tasks; however, the CE loss function does not consider the ordinal nature of labels. To address this issue, a suitable loss function should impose a greater penalty for predictions that deviate more from the true label than for those that are closer, unlike CE. For instance, the loss function should assign a higher penalty when a grade prediction model predicts A as D rather than as B.


Method : Distance Loss Function

The idea is from weighted mean square error, which is defined as follows:

\[L_{WMSE}(T, Y) = \frac{1}{nl}\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{l} w_{i} (T_{ij} - Y_{ij})^{2}\]

where $l$ is the number of labels, $n$ is the batch size, $T \in \mathbb{R}^{n \times l}$ is the target value, $Y \in \mathbb{R}^{n \times l}$ is the prediction of the regression model, and $w \in \mathbb{R}^{n}$ represents the weights.


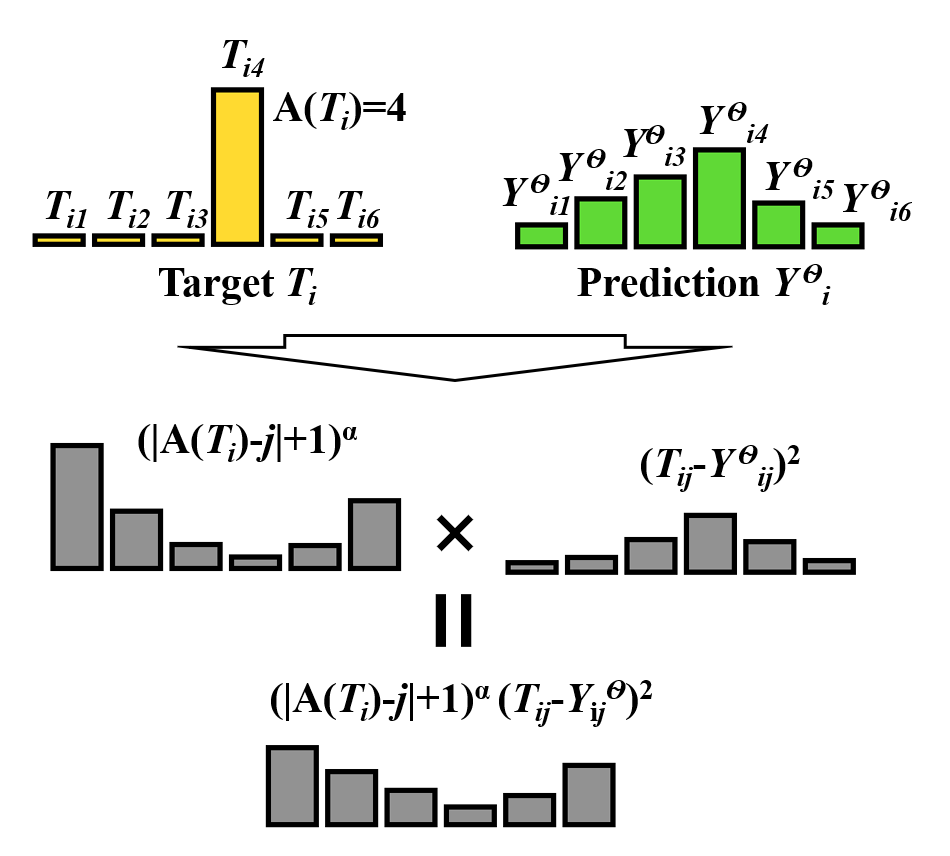
Figure 1. Example of distance mean-square (DiMS) calculation with six labels.


I propose a distance mean-square (DiMS) loss function motivated by the WMSE weight determination process. The DiMS loss function replaces weight $w$ in WMSE with the square of the distance to the target. DiMS loss function is defined as follows,

\[L(T, Y^{\theta};\alpha) = \frac{1}{nl}\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{l} (\lvert A(T_{i}) - j \rvert + 1)^{\alpha} (T_{ij} - Y_{ij}^{\theta})^{2}\]

where $ T \in \mathbb{R}^{l \times n} $ is the target matrix representing one-hot encoding, $ Y^{\theta} \in \mathbb{R}^{l \times n}$ is the prediction from a classification model with parameters $ \theta $, $\alpha$ is the hyperparameter that needs to be tuned experimentally, $ l $ is the number of labels, and $ n $ is the batch size. $T_{i}$ is an array consisting of zeros, except that $T_{ij}$ is $1$ when $j$ is the target index. $ A(T_{i}) $ represents the $ \arg\max $ of $ T_{ij} $, as shown below.

\[A(T_{i}) = \arg \max_{1 \leq j \leq l} T_{ij}\]

Details for DiMS

Herein, I explain why DiMS is more suitable than cross-entropy. The gradient of DiMS can be represented as,

\[\nabla_{\theta} L(T,\! Y^{\theta};\!\alpha)\!=\!\frac{-2}{nl}\!\sum\limits_{i=1}^{n} \!\sum\limits_{j=1}^{l} (\lvert A(T_{i})\!-j \rvert + 1)^{\alpha} \nabla_{\theta}(T_{ij}\!-Y_{ij}^{\theta})\]

I observe that the partial derivative of $ L(T, Y^{\theta}; \alpha) $ with respect to $ \theta $ is sensitive to the distance between labels. As the gap between the target $ T $ and $ Y $ increases, the gradient becomes significantly larger.

One of the main reasons why cross-entropy loss is not suitable for multiclass classifications is that it may cause the correct prediction to be updated to an incorrect prediction. Suppose a multiclass classification model predicts $[0.05, 0.1, 0.2, 0.4, 0.2, 0.05]$ from the true label $[0, 0, 0, 1, 0, 0]$. When I use the cross-entropy loss function to evaluate the model, I obtain a loss value of 9.39. In another case, the model predicted $[0.2, 0.1, 0.05, 0.4, 0.05, 0.2]$ from the same true label, which resulted in a loss value of 9.39 with the same loss function. Although $[0.4, 0, 0, 0.1, 0.2, 0.3]$ are close to the correct prediction, the model judges the two equally. However, in the ordinal classification, the prediction $[0.05, 0.1, 0.2, 0.4, 0.2, 0.05]$ is considered better.


Experiments

I experimented with DiMS loss function using deep neural network models and compared it with the other loss functions, CE, mean-square error (MSE), and order log loss functions under the same conditions. In previous studies, OLL exhibited a much better performance in ordinal classification than the others; therefore, I selected the OLL function for comparison.

I conducted the experiments using a custom dataset with $ \text{make} \text{regression} $ function in the scikit-learn package. I created 10000 data points with 99 features; among these, only 10 features were related to the target value. Subsequently, I separated the range of values and labeled them in increasing order. Thus, the dataset exhibited ordinal characteristics. I conducted the following experiments under certain conditions. First, the data were divided into training and test data at a ratio of 8:2. Second, each experiment was conducted with 5, 7, 10, 15, 20, 30, and 50 labels.


Labels CE MSE OLL$_{\alpha=1}$ OLL$_{\alpha=1.5}$ OLL$_{\alpha=2}$ DiMS$_{\alpha=1}$ DiMS$_{\alpha=2}$
5 95.4 97.1 94.7 96.6 96.6 97.1 97.1
7 89.0 91.7 93.4 93.4 92.3 96.6 96.5
10 83.2 91.0 89.2 89.6 89.0 94.7 94.6
15 77.7 86.6 82.0 84.9 83.9 92.5 92.3
20 72.7 82.2 75.6 79.4 78.9 89.8 89.9
50 39.9 58.3 62.6 58.8 55.7 73.3 73.2
Table 1. Benchmark of loss functions according to the number of labels. The text written in bold is the highest accuracy outside the error range of the 99% confidence interval.


As shown in Table 1, in the experiment with five labels, MSE and DiMS yield similar performances. DiMS exhibits better performance as the number of labels increase. Above a certain number of labels, DiMS performs slightly better than MSE and OLL. Additionally, as the number of labels increases, efficiency improves. Thus, DiMS shows a more robust performance, as there are more ordinal characteristics.

$\alpha$ is a hyperparameter used to tune the weight of the loss function. Because I do not know the degree of ordinal characteristics, it is difficult to optimize to obtain the best results. This determines how much value is weighted as the distance between classes increases. Therefore, I experimented with the effect of $\alpha$ on the scikit-learn custom dataset to determine the suitable alpha value.


$\alpha$ 0.3 0.5 1 1.5 2 2.5 3 5
5 96.5 96.8 97.1 96.9 97.1 97.0 97.2 97.1
7 95.7 96.2 96.6 96.7 96.5 96.7 96.3 96.0
10 93.3 94.3 94.7 94.7 94.6 94.6 94.4 93.1
15 91.0 92.3 92.5 92.3 92.3 92.0 91.8 87.3
20 89.4 90.4 89.8 89.9 89.9 89.6 88.6 77.5
50 78.8 78.6 73.3 76.7 73.2 67.8 61.7 32.8
Table 2. Experimental results of loss functions according to $\alpha$. The text in bold indicates the highest accuracy outside the error range of the 99% confidence interval.


Table 2 lists the performances of each hyperparameter $\alpha$ for various numbers of labels. Experiments showed that $\alpha$ should be adjusted. The best results were obtained when $\alpha = 0.3, 0.5, 1, 1.5, 2, 3$. However, when $\alpha$ is too large (for example, when $\alpha = 5$), it does not exhibit good performance. I recommend that the $\alpha$ value is tuned and chosen so that it ranges between 0.3 to 3 to achieve high performance. In addition, I found an interesting result when $\alpha$ was between 0.5 and 3: as the number of labels increased, a smaller $\alpha$ was more suitable for learning.

I demonstrate that DiMS is effective for text classification problems. I trained a language model on the full SST-5 dataset, which is commonly used in text classification problems. It is the most commonly used method for ordinal classification problems.


Model Score
BERT large 55.5
BCN + Suffix BiLSTM-tied + CoVe 56.2
GPT-2 + Heinsen Routing 58.5
RoBERTa large + Self-explaining 59.1
RoBERTa large + Heinsen routing 59.8
RoBERTa large + OSNN 61.1
RoBERTa large + OLL$_{\alpha=1}$ 61.0
BERT large + DiMS$_{\alpha=2}$ 56.8
RoBERTa large + DiMS$_{\alpha=2.5}$ 61.8
Table 3. Benchmark on SST-5. The text highlighted denotes the highest(new State-Of-The-Art) accuracy case/outcome.


As shown in Table 3, RoBERTa-DiMS$_{\alpha = 2.5}$ model sets a new state-of-the-art accuracy record in the SST-5 text classification task with an accuracy of 61.8. I only changed the loss function with the pretrained language model without any structural changes; it performed more effectively compared with the performances of previous studies. This shows that ordinal classification using DiMS is powerful, even for text classification problems. In addition, the previous record of the large BERT model in SST-5 was 55.5; however, I set a better record in the case of the large BERT model with DiMS, with a record of 56.8. Moreover, when the aforementioned techniques for language modeling are applied, better performance is expected.