Race Strategy Optimization by using Genetic Algorithm
Simulation, Optimization
- Project GitHub Repository : HERE
- Date : 2023.10.22 ~ 2023.10.26
- Writter : 9tailwolf
Project Overview
In Formula 1, strategy is a importance element for making the best result in racing. Today, sports strategy engineers study various strategies to win games. One of the most well-known algorithm is a Genetic Algorithm, which is the most useful artificial intelligence problem solving method before Neural Network became popular. In this page, I apply basic genetic algorithm in formula1 to optimize the race strategy with practice session datas.
Genetic Algorithm
A genetic algorithm is a search heuristic that is inspired by Charles Darwin’s theory of natural evolution. This algorithm reflects the process of natural selection where the fittest individuals are selected for reproduction in order to produce offspring of the next generation.
Following is a pseudocode of the genetic algorithm.
- Initial Population
- Measure
- Selection
- Crossover
- Mutation
- Repeat steps 2 to 6 until find enough solution.
Note that genetic algorithms do not always find the optimal solution.
Agenda
tire Compound
A tire compound defines the type of tires. We should know that there is a 3 types of dry condition tires.
-
Soft: Soft tire has the highest grip and can make the best performance of the car, Instead of performance, durability is the worst. -
Medium: Medium tire has a good grip so it can make the good performance. Durability of the tire is also good. -
Hard: Hard tire has the lowest grip and can make the longest performance of the car, Instead of performance, performance is the worst.
And there are 2 more compound for wet condition.
-
Intermediate: Intermediate tire is fit for slightly rainy environment. -
Wet: Wet tire is fit for rainy environment.
Fuel
Every car use a different quantity of fuel. The car must use under 110kg of fuel, without refueling. Fuel use can make better performance, but vehicle weight decrease performance.
Pit-Stop
Pit stops are mandatory once in f1. It is essential to use two types of tires. Depending on when and how often tires are changed, overall lap time is affected.
In addition to this, other points to consider are as follows:
- Weather
- Temperature
- Battle for other drivers
- DRS
- Penalties
- Safety Car
You can see linked pages for more information.
Algorithm
Fitness Function
The best strategy is the one with the lowest laptime. We need the process that estimate laptime with tire. I aim to find the best solution with practice session data. In this genetic algorithm model, I suppose that the factors which affect laptime are three, tire compound, Fuel, and Pit-Stop. In this way, total time can be below.
Because practice session data consists of fuel and tire data, \(t_{tire, i} + t_{fuel, i}\) can calculate at once. So I apply regression with practice session data.
Regression
I surpose that tire age-tire wear function will be cubic function, \(t_{tire}(l) = al^{3} + bl^{2} + cl + d\). Simillary, I supporse that fuel-laptime function will be linear. As a result, Regression model can be below.
\[f_{tire,fuel} : Y = ax_{1}^{3} + bx_{1}^{2} + cx_{1} + d + ex_{2}\]And I assume some conditions.
- $ t_{laptime} = \frac{t_{ideal}}{f_{tire,fuel}} $.
- When tire wear rate is $40\%$($X_{1 ideal}$), then $f_{tire,fuel}$ is $92\%$($Y_{ideal}$) of the $t_{ideal}$.
- At that point, $\frac{df}{dX_{1}} = 0$ and $\frac{d^{2}f}{d(X_{1})^{2}} = 0$
- Therefore, $a = \frac{(92-t_{ideal})}{X_{1 ideal}^{3}}$, $b = -\frac{3}{2}aX_{1 ideal}$, $c = \frac{3}{2}aX_{1 ideal}^{2}$, $ d = t_{ideal}$ in initial coefficient of regression.
Below is a partion code of regression.
def regression(self):
minimum_fuel_usage = self.mean_fuel_usage * 0.9
a = (92 - self.ideal_lap) / self.estim_laps ** 3
b = -3 * a * self.estim_laps * 0.5
c = 3 * a * self.estim_laps ** 2 * 0.5
d = self.ideal_lap
e = 1 # Unknown
for _ in tqdm(range(self.lt),desc=self.compound + ' Compound Regression'):
y = a * self.X1 ** 3 + b * self.X1 ** 2 + c * self.X1 + d + e * (self.X2 - minimum_fuel_usage)
a_grad = sum((self.X1 ** 3) * (y - self.Y)) / len(self.X1)
b_grad = sum((self.X1 ** 2) * (y - self.Y)) / len(self.X2)
c_grad = sum((self.X1) * (y - self.Y)) / len(self.X1)
d_grad = sum((y - self.Y)) / len(self.X1)
e_grad = sum(self.X2 - minimum_fuel_usage) / len(self.X2)
a = a - self.lr * a_grad
b = b - self.lr * b_grad
c = c - self.lr * c_grad
d = d - self.lr * d_grad
e = e - self.lr * e_grad
time.sleep(0.0001)
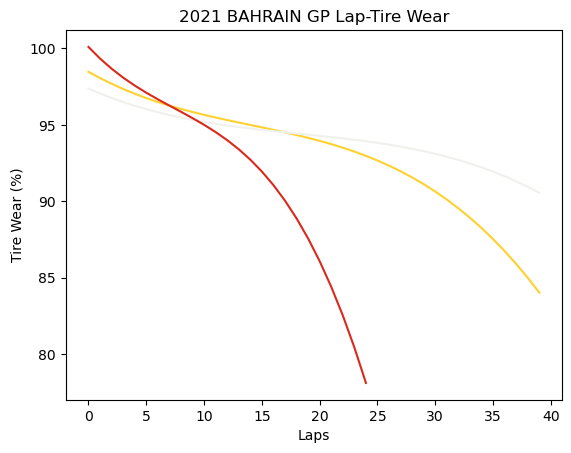
return a, b, c, d, eFor example, as a result, below is a tire age-tire wear grpah in 2021 Bahrain Grand Prix, Tire age-tire wear grpah is below.
1. Initial population
At first, I set initial population randomly. Any strategy can be determined in a limited range. Below is my limitations.
- Initial population : 100
- Max pitstop : 4
- Fuel range : 100~110
- Tire compound : Soft, Medium, Hard (In my case, I didn’t consider weather.)
2. Selection
At selection Step, Algorithm choose the good strategies in population by using fitness function. In my case, I choose 20 strategies that make a good laptime.
3. Crossover
In the Crossover step, new children are created between the objects selected in the Selection step. Here’s how to create a new child.
- Exchange one tire at random.
- Corrects the oldest and youngest tires by a random number (0,1,2,3,4,5).
- The oldest tires are subtracted and the youngest tires are added.
- Fuel is exchanged.
In my case, I made 40 strategies in crossover step.
4. Mutaion
The mutation step goes through the following processes.
- Pit stops are added or omitted at random.
- Fuel is adjusted arbitrarily.
- The order of tires is randomly reversed.
In my case, I made 40 strategies in mutaion step.
Below codes are all process of the genetic algorithm.
class Genetic:
def __init__(self, path:str, initial_population_size:int, lap:int, pit_time:int,max_pitstop:int, selection_size:int, crossover_size:int, mutation_size:int, iteration:int):
self.initial_population_size = initial_population_size
self.lap = lap
self.pit_time = pit_time
self.max_pitstop = max_pitstop
self.fuel_range = (100,110)
self.fitting_function = LaptimeCalculator(path)
self.selection_size = selection_size
self.crossover_size = crossover_size
self.mutation_size = mutation_size
self.iteration = iteration
self.population = None
self.best_performance = 10**5
self.best_strategy = None
self.possible_strategy = find_possible_strategy(self.max_pitstop)
self.save_results = {i:None for i in self.possible_strategy}
self.save_performance = {i:10**5 for i in self.possible_strategy}
def initial_population(self, pitstop, fuel):
return strategyGenerator(self.initial_population_size, self.lap, pitstop, fuel)
def fitness(self,strategy):
return self.fitting_function.calculation(strategy.decoded_strategy,strategy.pitstop,self.pit_time)
def compute_performance(self):
performance = []
for i in self.population:
performance.append((Strategy(i.encoded_strategy,self.lap), round(self.fitness(Strategy(i.encoded_strategy,self.lap)),4)))
sorted_population = sorted(performance, key=lambda x: x[1])
return sorted_population
def selection(self, performance):
better_strategies = performance[:self.selection_size]
better_strategies = [i[0] for i in better_strategies]
return better_strategies
def crossover(self, sub_population):
crossovered_popupation = []
for _ in range(self.crossover_size):
parent1,parent2 = random.randint(0,self.selection_size-1), random.randint(0,self.selection_size-1)
crossovered_popupation.append(sub_population[parent1] + sub_population[parent2])
return crossovered_popupation
def mutation(self, population):
mutation_population = random.sample(population, self.mutation_size)
for i in range(self.mutation_size):
mutation_population[i] = mutation_population[i].mutate(self.max_pitstop,self.fuel_range)
return mutation_population
def generation(self):
performance = self.compute_performance()
selected_population = self.selection(performance)
crossover_population = self.crossover(selected_population)
new_generation = selected_population + crossover_population
mutation_population = self.mutation(new_generation)
population = new_generation + mutation_population
self.population = population
def run(self,result_size):
self.population = self.initial_population(self.max_pitstop, self.fuel_range) # initial
for _ in tqdm(range(self.iteration),desc='Genetic Algorithm'):
self.generation()
time.sleep(0.002)
res = [self.save_results[i] if self.save_results[i] else(None,10**5) for i in self.possible_strategy]
res.sort(key=lambda x:x[1])
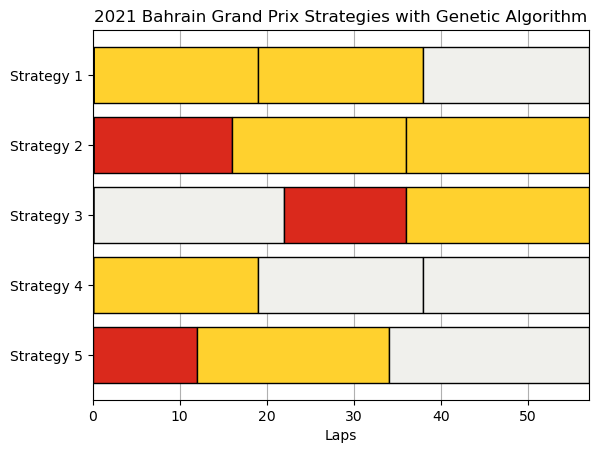
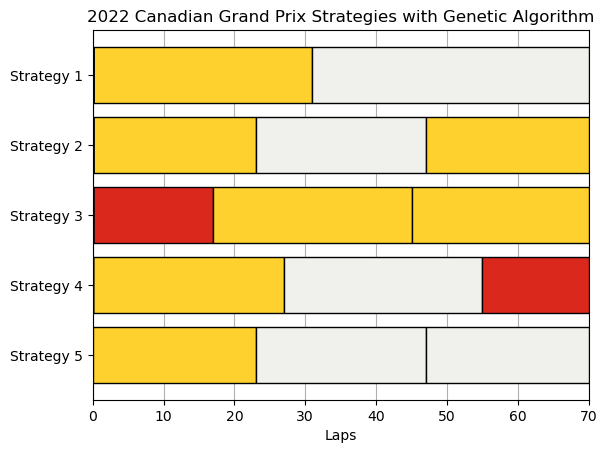
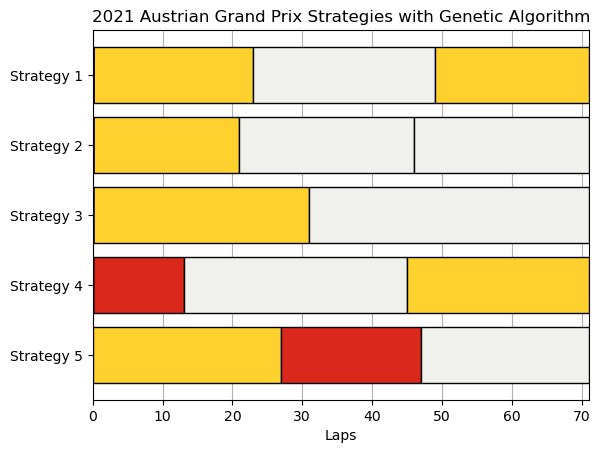
self.print_result(res,result_size)Comparison Result
2021 Bahrain Grand Prix
2022 Canadian Grand Prix
2021 Austrian Grand Prix

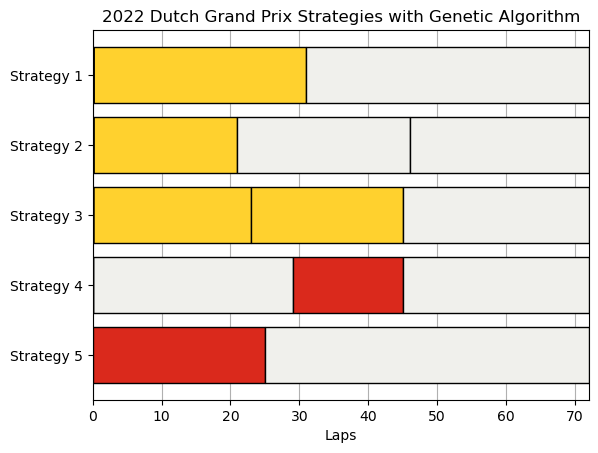
2021 Dutch Grand Prix